- 遺伝的アルゴリズムってどんなAIなの?
- どういう問題を解決するのに向いているの?
- 実際の活用例って何があるの?
遺伝的アルゴリズムは、生物の生殖と遺伝の継承、適者生存よる自然淘汰などの生物の進化の仕組みを模倣するアルゴリズムです。
これだけ聞いても何のことか分からないと思いますが、今のところは、生物が遺伝子を交換して子を作ることで環境に適応するように進化してきた過程をコンピューター上で模倣して、とある問題にアプローチすると考えて下さい。
私はディープラーニングや遺伝的アルゴリズムの勉強を始めた時に、既にある程度の数学知識のある方向けや技術者向けの記事が多く、学習に苦労した覚えがあります。
そこで遺伝的アルゴリズムとはどんなAIなのか…AIについて興味を持ち始めた方、遺伝的アルゴリズムを使ったAIをプログラミングしてみたい方向けに、分かりやすく解説していきます。
目次
遺伝的アルゴリズムとは?
遺伝的アルゴリズム(Genetic Algorithms:GA)は、生物の進化の仕組みを模倣するアルゴリズム(※)で、この仕組みを使うことで、組み合わせ最適化問題を解くことができます。
※アルゴリズムとは、手順や計算方法のこと。
これだけでは何のことが分からないと思うので、次のことをもう少し深堀して解説します。
- 生物の進化の仕組みについて
- 組み合わせ最適化問題について
- 遺伝的アルゴリズムを使うメリット
遺伝的アルゴリズムの具体的な処理の流れについては、『遺伝的アルゴリズムの流れ』で解説しています。
生物の進化の仕組みについて
我々人間含め生物は、遺伝子を交換して子を作ることで遺伝子を次の世代に継承し、適者生存よる自然淘汰により、環境に適応できるように進化してきました。
環境に適応できなかった遺伝子を持った個体は、早くに亡くなったり、子を残せなかったりするため、その遺伝子が継承されず無くなってしまいます。
これを自然淘汰と言うのですが、それを何世代も繰り返すことで環境に適応できる遺伝子が残り続けます。
1世代で遺伝子が大きく分かるものでは無いので、これを数百、数千世代と途方もない世代で繰り返し、環境に適した遺伝子となります。
この仕組みをコンピューター上で再現して、組み合わせ最適化問題を効率よく解くのが遺伝的アルゴリズムというAIです。
組み合わせ最適化問題について
例えば、スーパーなどで3000円以内でできるだけたくさん食べれるようにグラム数の大きいものを買いたい場合、どの商品を買えばグラム数を最大化できるかを考えた時に、様々な商品の中から組み合わせを考える必要があります。
このように、目的に合わせて膨大な組み合わせから最適な解を探す問題を組み合わせ問題と言います。
商品毎にグラム数が決まっているので、グラム数が多くなる組み合わせを探すことになります。
商品数が10点ぐらいの中から選ぶのであれば、それほど組み合わせはないので自分で計算することができます。
厳密に計算しなくても、大体こんな感じかな…と見た感じで選んでもある程度いい感じにグラム数の多い組み合わせを見つけることができると思います。
しかし、商品数が1000点と膨大になった時、自分で計算するのは不可能ですし、商品毎のグラム数のデータを持っていて、コンピューターで計算できたとしても、総当たりで計算していくには無理があります。
遺伝的アルゴリズムを使うメリット
遺伝的アルゴリズムを使う最大のメリットは、組み合わせ問題において、”いい感じ”の答えを比較的”短時間”で見つけ出すことができる点です。
組み合わせ問題は、要素が多くなると指数関数的に組み合わせ数が多くなる特徴があります。
そのため、総当たりで演算をして解を比較して最良の解を求める方法では、早い段階で演算能力に限界が来て、現実的な時間内では計算が終わらないという結果になります。
実際にイメージして頂けるように、遺伝的アルゴリズムでよく例題になる『巡回セールスマン問題』で、どのくらいの要素数で、どのくらいの組み合わせ数になるのか確認してみましょう。
巡回セールスマン問題については後程解説しますが、簡単に言うと、セールスマンが都市を1回ずつ訪問して最初の都市に戻ってくる場合に、移動距離が最小になる組み合わせを求める問題です。
例えば、A, B, C, Dの4つの都市があった場合、次のような組み合わせが考えられます。
① A ⇒ B ⇒ C ⇒ D ⇒ A
② A ⇒ B ⇒ D ⇒ C ⇒ A
③ A ⇒ C ⇒ B ⇒ D ⇒ A
※順番を逆にした道順は省いています。
3通りであれば簡単に計算することができますが、都市の数が増えると指数関数的に組み合わせが増えます。
都市の数毎の巡回ルートの組み合わせ数
| 都市数 | 組み合わせ数 |
|---|---|
| 4 | 3 |
| 5 | 12 |
| 6 | 60 |
| 7 | 360 |
| 8 | 2,520 |
| 9 | 20,160 |
| 10 | 約18万 |
| 15 | 約430億 |
| 17 | 約10兆 |
| 20 | 約6京 |
都市Aから開始するという前提条件がありますが、これが無ければもっと多くなります。
都市数が4つ、5つあたりであれば自分で計算できるかもしれませんが、それ以降はコンピューターを使わないと計算は難しい数になってきます。
都市数が15になると約430億通りになるので、総当たりで計算する場合、コンピューターであっても数週間、数カ月はかかるでしょう。
計算が終わらないわけではないですが、現実的な時間内に計算が完了するとは言い難いです。
実際に遺伝的アルゴリズムで問題を解こうとした時に、要素数が15個に収まるわけはありません。
また、組み合わせごとに結果を評価する必要がありますが、総移動距離と比較的簡単な計算では無く、もっと複雑で時間のかかる計算を必要とする場合もあります。
これを含めて考えると、組み合わせ最適化問題は、早い段階で現実的に計算できない組み合わせ数となるので、総当たりで解を導き出すのに効率的とは言えません。
近年コンピューターの性能はどんどん向上しており計算できる上限は増えてはいるものの、その性能で計算できる限界を優に超える数を計算することになります。
そこで、要素が多くても現実的な時間内に解を導き出すために使われるのが遺伝的アルゴリズムです。
遺伝的アルゴリズムを使うことで、全ての組み合わせを計算することなく、短時間で解を導き出します。
ここで注意しておきたいのは、遺伝的アルゴリズムは、全ての組み合わせを計算して解を比較するわけではないので、最も良い解(=厳密解)は求めることができません。
厳密解ではないけれども、最も良い解に近い、いい感じの解(=近似解)を比較的短時間で求めることができます。
遺伝的アルゴリズムの例題
遺伝的アルゴリズムを説明する際によく使われる例題があります。
- 巡回セールスマン問題
- ナップザック問題
特に、巡回セールスマン問題は、遺伝的アルゴリズムを勉強する上で、絶対と言っていいほど出てくるので、どういうものか解説しておきます。
巡回セールスマン問題
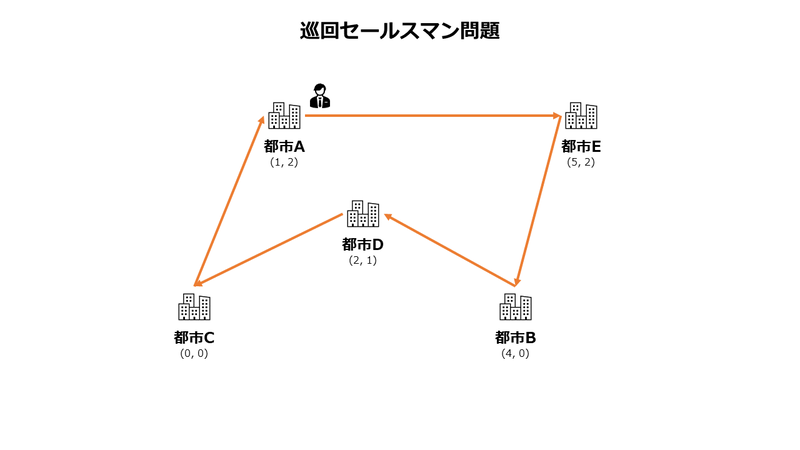
巡回セールスマン問題とは、セールスマンがある都市から出発して、全ての都市を1回ずつ訪問して最初の都市に帰ってくるまでにかかる総移動距離が最小になるように、どういう順番で訪れれば良いかを求める組み合わせ最適化問題です。
 ケンさん
ケンさん
図のように色々な場所に都市があり、都市間を直線で移動できるものとします。
都市が4つあるので組み合わせとしては3通りです。
訪問する都市順にリストにすると次のように示すことができます。
① A ⇒ B ⇒ C ⇒ D ⇒ A
② A ⇒ B ⇒ D ⇒ C ⇒ A
③ A ⇒ C ⇒ B ⇒ D ⇒ A
1行ごとに1つの組み合わせで、1つ目の『A ⇒ B ⇒ C ⇒ D ⇒ A』で言うと、都市Aから始まり、都市B、都市C、都市D、最後に都市Aに戻ってくるという流れです。
この組み合わせが3通りあります。
都市の座標は分かっているので、三平方の定理を使って2つの都市間の距離を求めることができます。
これを全ての都市間で行い合計したものが総移動距離となり、この問題では総移動距離が短い方が優秀な組み合わせとなります。
総当たりで計算してくこともできますが、都市数が多くなると膨大な時間が掛かるので現実的ではありません。
総当たりに対して、遺伝的アルゴリズムでは、徐々に優秀な組み合わせのみを選択していく仕組みになっているので、全ての組み合わせを試すことなく解を出すことができます。
最初はランダムで生成した組み合わせを計算するので、良い組み合わせ、悪い組み合わせが混ざりますが、その中から良い組み合わせを選択しています。
2つの良い組み合わせ掛け合わせて、新しい組み合わせを作って評価するので、より総移動距離の短い組み合わせが出てくるというわけです。
ナップザック問題

ナップザック問題とは、ナップザックの中に品物を詰める際に、詰めた品物の価値を最大化するための組み合わせを選ぶ問題です。
品物の価値とは値段で、品物毎の寸法や重量は分かるものと考えて下さい。
この問題では、ナップザックの容量、寸法に収まるように考える必要があります。
また、組み合わせによっては品物の数も変わってくるので、この点も難しいポイントですね。
遺伝的アルゴリズムの活用例
例題だけではなく、実際に遺伝的アルゴリズムが活用された例も解説しておきましょう。
代表的なものが次の2つです。
- N700系の先端部分の形状
- 人工衛星のアンテナの形状
N700系の先端部分の形状

2007年に登場したN700系の先頭部分の空力設計をする際に、遺伝的アルゴリズムを用いて約5,000パターンのコンピューターシミュレーションを行って、デザインが決定されました。
ただ空気抵抗を減らし速くなるための設計ではなく、微気圧波を減らすためのデザイン設計が必要だったようです。
微気圧波とは、トンネルに突入した際に、トンネル内の空気が拡散しないため、空気が圧縮され衝撃波のようになり、出口部分で解放されたときに大きな衝撃や音を発生させる現象のことです。
この衝撃や音が大きいと周辺地域の住民にとって騒音になるので、それを解消するための形状を探し出す必要があったようです。
先頭車両の乗車人数や長さなど様々な制約がある中で、微気圧波を減らすために、遺伝的アルゴリズムを使って効率よく適した形状が探し出されたわけですね。
より詳しく知りたい方は、下記の記事を参考にしてみて下さい。
≫ 参考記事:新型新幹線「N700系」の“顔”を生んだ「遺伝的アルゴリズム」の秘密【その2】
人工衛星のアンテナの形状

ST5で行われた技術試験計画の中で衛星に搭載されたアンテナの形状が遺伝的アルゴリズムによって設計されました。
ST5とは、Space Technology 5の略で、NASAのニュー・ミレニアム計画の一環として行われた3基の小型衛星で行われた技術試験計画のことです。
画像は、最終的に指定された仕様に最適な形へと進化したアンテナです。
画像を見てもわかるように、かなりぐにゃぐにゃとしていて人間の設計では到底思いつかなさそうな形状をしています。
どういう項目が評価基準となって、この形へと進化していったのかは分からないですが、アンテナから送信される電波の形などが複雑なので、どういう形状にすればより広範囲に電波を届けることができるか、などの観点から効率的に形状を探すために遺伝的アルゴリズムが使われたのだと思います。
≫ 参考文献:Automated Antenna Design with Evolutionary Algorithms(英語)
遺伝的アルゴリズムの流れ
遺伝的アルゴリズムがどういうAIで、どんな問題にアプローチできるのか、例題や活用例を紹介しつつ解説しました。
ここからは、これから遺伝的アルゴリズムを使ったAIをプログラミングしてみたい方向けに遺伝的アルゴリズムの処理の流れを解説していきます。
遺伝的アルゴリズムの実装には、Pythonでサンプルコードがたくさんあるのですが、遺伝的アルゴリズムの全体の流れを知っておかないと、コード上で何をしているのか理解できません。
その理解をスムーズにするために、分かりやすく遺伝的アルゴリズムが何をやっているのか解説していきます。
イメージしやすいように例題の『巡回セールスマン問題』を使いつつ解説していきます。
遺伝的アルゴリズムの全体的な流れ
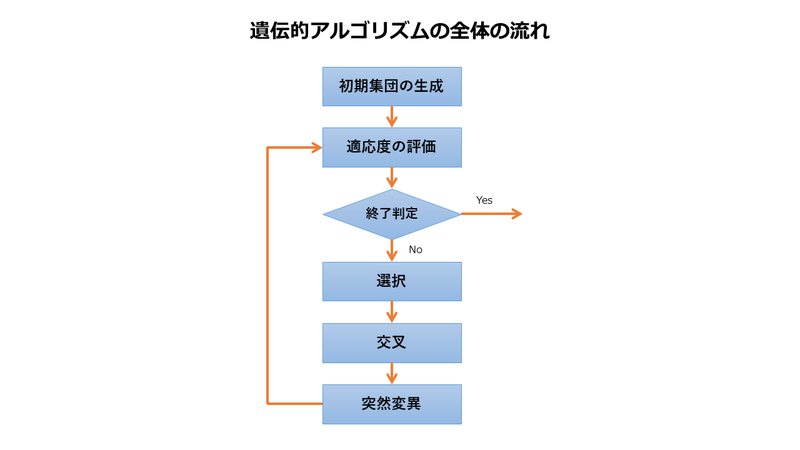
遺伝的アルゴリズムの全体的な処理の流れはこのような感じです。
ランダムに生成した初期集団の個体(=1つの組み合わせ)に対して、適応度を評価します。
巡回セールスマン問題では、移動距離が最小になる組み合わせを求めるので、適応度の評価は、その組み合わせの総移動距離となります。
終了判定は、遺伝的アルゴリズムの学習を終了するかどうかです。
世代数であったり、学習時間であったり、満足のいく適応度に到達した段階で終了します。
選択では、親となる優秀な個体を選択します。
この個体が次世代の子となる個体を生成する際の元になります。
様々な選択方法がありますが、巡回セールスマン問題であれば、「総移動距離が短い方が効率的に巡回できる=優秀な個体」なので、移動距離が短いものが対象となります。
交叉では、2つの親の個体から、遺伝子の一部を入れ替える操作をして、2つの子となる個体を生成します。
優秀な親から子を生成することで、子もランダムで生成するより良い結果になることがイメージできると思います。
ここが組み合わせ最適化問題を総当たりで計算していくより、遺伝的アルゴリズムを使うことで効率的に良い組み合わせを探し出すことができる重要なポイントとなります。
突然変異は、少ない確率で遺伝子の一部をランダムに変化させます。
生物の世界でも、遺伝的な突然変異によって、同種の個体とは違う個体が生まれることがありますが、それと同じです。
突然変異させることで、局所解に陥ることを防ぐ効果があります。
局所解とは、本当は別に最適な解があるにも関わらず、部分的な最適な解に収束してしまうことです。
適応度の評価から突然変異までを1世代とカウントし、交叉によって生まれた子の集団が次世代となります。
これを100世代繰り返したり、満足のいく適応度の解が見つかるまで繰り返したりします。
実際にプログラミングする際は、画像の項目の通りに、全体の流れとなる関数と各処理の関数を作って、全体の流れとなる関数内で、各処理の関数を実行していくようなイメージです。
最初に述べた通り、遺伝的アルゴリズムは、生物の進化の仕組みを模倣するアルゴリズムです。
親から遺伝子を受け継ぎ、環境に適さない遺伝子を持った個体は自然淘汰され、環境に適した遺伝子を持った個体は生き残ることができます。
この仕組みを組み合わせ最適化問題を効率的に解くために利用したのが、遺伝的アルゴリズムです。
遺伝的アルゴリズムの全体的な流れを解説しましたが、次はそれぞれの処理を詳しく見ていきましょう。
初期集団の生成
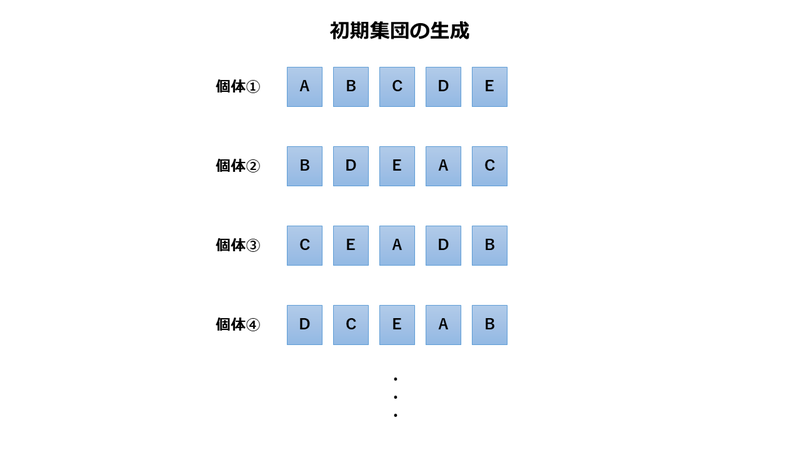
初期集団の生成は、ランダムに生成した組み合わせを50個、100個と複数生成します。
いくつ生成するかは、全体の組み合わせ数などによって異なってくるので、色々試して調整すると良いでしょう。
組み合わせ問題ごとに、遺伝的アルゴリズムで扱えるような遺伝子配列にデータを整理する必要があります。
エンコーディングと呼ばれますが、主に次の方法があります。
| エンコーディング方法 | 概要 | 例 |
|---|---|---|
| 実数値エンコーディング | 各遺伝子を数値・文字で表現する。 | 個体①:2, 0.6, 8, 0.25, 54, 0.45 個体②:0.25, 7, 0.64, 6, 0.71, 8 |
| 順列エンコーディング | 各遺伝子を順番を表す番号で表現する。 巡回セールスマン問題などの順番を 並び替える問題などで使われる。 | 個体①:573842196 個体②:975148326 |
| バイナリエンコーディング | 各遺伝子を「0」と「1」の2進数で表現する。 | 個体①:1011101011 個体②:0010100100 |
問題にあった方法で、遺伝的アルゴリズムが扱えるデータに変換します。
適応度の評価
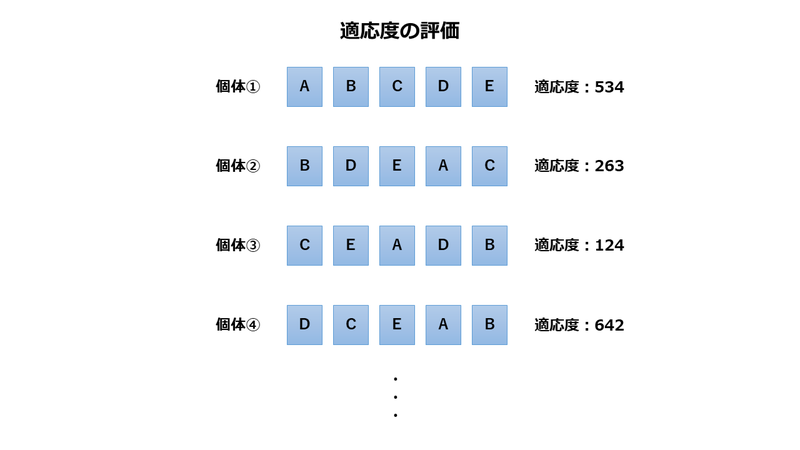
適応度の評価は、その組み合わせで問題を解いた時の答えを計算します。
この計算は、遺伝的アルゴリズムの学習の方向性を決める重要なもので、問題ごとによって全く違います。
巡回セールスマン問題では、移動距離が最小になる組み合わせを求めるので、適応度の評価は総移動距離となります。
具体的には、三平方の定理を使って、2つの都市の座標から距離を求めます。
これを全ての都市間で行い合計したものが、適応度となります。
この問題の場合は、移動距離が短い方が効率的に全ての都市を訪問でき、優秀な組み合わせとされるので適応度が小さい方が優秀ですね。
適応度は次の選択の際に使うのですが、高い方が優秀とするのが一般的なので、解説の都合上、高い=優秀とします。
選択
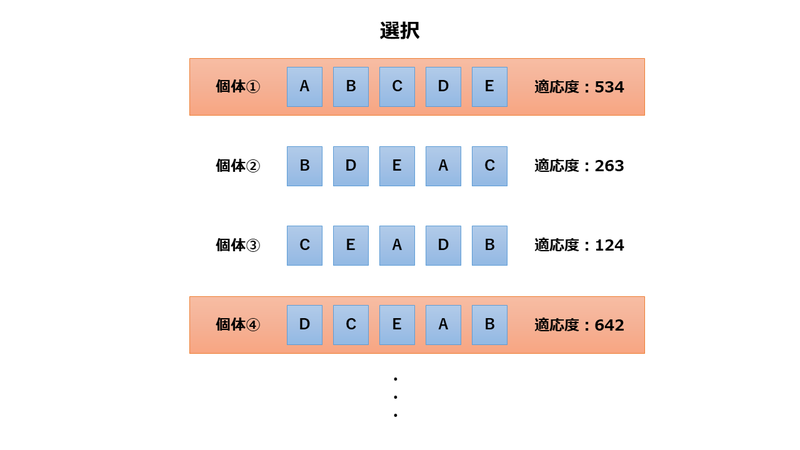
選択は、適応度を元に次世代の親となる優秀な個体を選択します。
選択方法は、主に次のようなものがあります。
| 選択方法 | 概要 |
|---|---|
| トーナメント選択 | 集団からランダムに数個の個体を選択して、 その中から適応度が最も高い個体を残します。 これを必要な個体数まで繰り返します。 |
| ルーレット選択 | 適応度を元に選択される確率を決めます。 適応度が高いほど選択される確率が高くなり、 優秀でない個体も含まれるため、多様性がなくならず、 しかし、個体の適応度の差が大きすぎる場合は、 |
| ランキング選択 | 適応度の”順位”を元に選択される確率を決めます。 ルーレット選択と違い、個体の適応度の差が大きすぎる場合でも、 |
| エリート選択 | 適応度の高い順に選択します。 優秀な個体が残るため早く収束しますが、 |
選択方法によってメリット・デメリットがあり、問題によってどれを採用すべきかは異なってきます。
そのため、世代毎の平均適応度の伸び具合が低く異様な場合は、他の選択方法も試す必要があります。
交叉
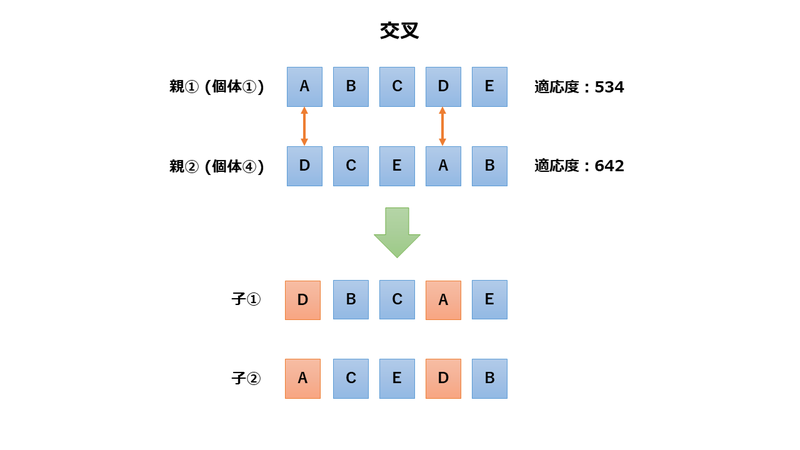
交叉では、2つの親の個体から、遺伝子の一部を入れ替える操作をして、2つの子となる個体を生成します。
交叉方法は、主に次のようなものがあります。
| 交叉方法 | 概要 | 変更前 | 変更後 |
|---|---|---|---|
| 一様交叉 | 一定の確率で各遺伝子を交換する。 | 親個体①:1011101011 親個体②:0010100100 | 子個体①:1010100000 子個体②:0011101111 |
| 一点交叉 | 1つの交叉点をランダムで選び、 それ以降の遺伝子を交換する。 | 親個体①:1011101011 親個体②:0010100100 | 子個体①:1011100100 子個体②:0010101011 |
| 二点交叉 | 2つの交叉点をランダムで選び、 その間の遺伝子を交換する。 | 親個体①:1011101011 親個体②:0010100100 | 子個体①:1011100111 子個体②:0010101000 |
| 多点交叉 | 3つの交叉点をランダムで選び、 その間の遺伝子を交換する。 | 親個体①:1011101011 親個体②:0010100100 | 子個体①:1010101000 子個体②:0011100111 |
一点交叉と多点交叉については、効率が良くなくあまり用いられていません。
私は良く一様交叉を使って実装することが多いのですが、これも色々試してみると良いでしょう。
また、問題によってはこのように単純に交換することができない場合があります。
例えば、巡回セールスマン問題であれば、単純に組み替えてしまうと同じ都市を訪問する可能性が出てくるので、この制約がクリアできるような方法で交叉する必要があります。
突然変異
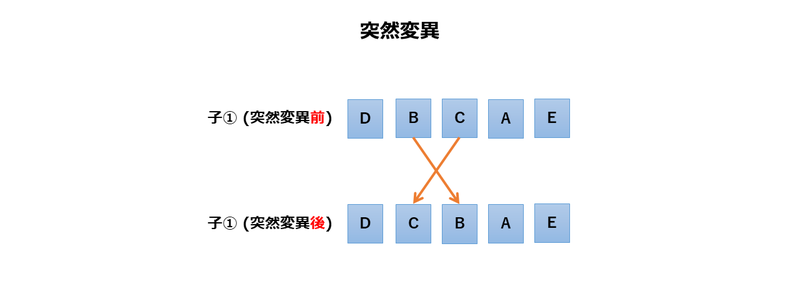
突然変異は、少ない確率で個体の遺伝子の一部をランダムに変化させます。
確率としては、0.1%~1%(100~1000個に1個)程度です。
この確率で突然変異の対象となる個体を選び、さらにその個体の遺伝子の一部を変化させます。
突然変異を入れることで、局所解に陥ることを防ぐ効果があります。
しかし、確率が低すぎると局所解になりますし、確率が高すぎると解が収束しにくくなるので、都度調整が必要になる場合があります。
まとめ:組み合わせ問題には遺伝的アルゴリズム
遺伝的アルゴリズムがどういうAIで、どういった問題を解くための適したAIか、また、例題や活用例、処理の流れを解説しました。
遺伝的アルゴリズムは、生物の進化の仕組みを模倣するアルゴリズムで、組み合わせ最適化問題を解くことができます。
組み合わせ最適化問題の最大の難点は、要素数が増えると指数関数的に組み合わせ数が増えるため、総当たりで計算していくと、現代のコンピューターでは現実的な時間内に計算が終わらないことです。
これを比較的短時間で解を導き出せるのが遺伝的アルゴリズムです。
AIについて勉強する前は、人工知能で何でもできる便利なものというイメージがあったのではないでしょうか?
実際は、AIごとにアプローチできる問題がある程度決まっており、遺伝的アルゴリズムの場合は組み合わせ最適化問題です。
意外とできることは少ないんだな…という印象を持ったかもしれませんが、それでもAIを使えるか否かで、実現できるプログラムの幅は大きく変わります。
人間には到底できない精度、速度で問題を解くことができるようになるので、このスキルを身に付け、自由自在に使いこなせるようになれば、プログラムでできることが格段に増えます。
ぜひ、自分でも遺伝的アルゴリズムを使ったプログラムに取り組んでみましょう。